Surface Excess in Solution Chemistry Has
Been Missed.
To
the memory of my parents, Almudena and Federico.
Some
G, g, and d symbols in the text must be read as Gamma (uppercase),
gamma (lowercase) and delta (lowercase). While the blod editor supports
many features, it des not seem to support Symbol font characters. The
author.
The
surface excess of chemicals in solution may be shaping several
properties of solutes, like the solubility equilibria of sparingly
soluble salts and the optical properties of solutions with
significant surface excesses. Activity coefficients can be regarded
as a ratio between the actual surface excess and the theoretical
surface excess if the ratio excess to bulk concentration was
maintained. A model is presented, based on the theoretical
proposition by Petersen and Saykally that cationic and anionic
components of Ray-Jones salts must form separate subsurface
excesses. It regards such surface excesses as charged planes and
considers that solubility products and other equilibrium conditions
are based of a Bjerrum-like critical distance. If the surface charge
density between the charge planes of the subsurface excesses is
large enough, electrostatic forces cause the ions to approach and
react. The model is consistent with the mathematical form of
deviations from ideal behavior in colorimetric methods. It is
suggested that non-zero order kinetic equations are also linked to
both plane concentrations and surface renewal due to agitation. It
is shown how the equations of this model have the same aggregate
shape than conventional action mass models and their adjustments for
non-ideal behavior, showing why misconceptions on the fundamental
chemistry of many processes in solution have been covered by the
fact that sufficiently effective predictive models were being
developed based on wrong postulates.
1.
Introduction
1.1.The
Weierstrass Snare.
The
Weierstrass Theorem states in one of its forms that any continuous
function over an interval can be described by a polynomial function.
Trivially,
the result of altering the original function by incorporating another
continuous function (e.g. a model refinement) would still be
described by another polynomial function. Eventually, a highly
refined model could be produced, and it would be possible to replace
it by a polynomial series. After all, all physicochemical problems
are investigated with the help of computers, and this is how complex
equations are ultimately fed to computers.
As
a consequence, if the initial function was chosen by making the wrong
starting hypothesis, and the corrections are based on a
misinterpretation of the problem, this will be disguised by the
validity of the results. This may lead to complacency and the belief
that a solid scientific knowledge has been attained. We can call this
the Weierstrass Snare.
However,
the polynomial approximation of the aggregate equation or function
obtained will be also be that of the aggregate form of the real model
for the system. Therefore, if a new model is proposed that deals with
behaviours previously regarded as anomalous, as predictable and
mainstream cases of the new model and the overall form of the new
model is consistent with either the original or polynomial forms of
the “numerically efficient” existing model, then there will be
strong evidence to support the idea that the new model deals better
with the description of reality.
1.2.
On the idea that some of the solution chemistry is controlled by the
surface excesses of solutes.
At
25oC
it is possible to have 70.1 kg of AgNO3
mixed with 29.9 kg of H2O
[3]. The average distance between
two ions of opposite charge on the basis of each occupying a cubic
cell is 2.9 nm. The amount of water required to have Ag(H2O)2
hydrates in that mixture would account for half of the water. This
indicates that such system's solubility is defined in the bulk phase.
But only about 50 gram of AgCl can be dissolved in the same 29.9 kg
of water[1]. Evidence in favor of the idea that this is the
consequence of formation at a singularity (like the surface of the
liquid) of a stable, insoluble product will be presented, based on
the idea that the behavior of ionic surfactants can be related to
that of other ionic solutes.
Ionic
surfactants are central to this study because their surface
tension-modifying properties makes it easier to quantify their
surface excesses. Their precipitation from diluted solutions takes
place with the surfactant present as a monomer with a “normal”
solubility product like, for example [2,3]
[Ca2+][DDBS-]2
= 2 10-11
[Al3+][DDBS-]3
= 4 10-19
[Ag+][DS-]
= 6.3 10-5
[Cu2+][DS-]2
= 7.9 10-19
[La3+][DS-]3
= 6.3 10-14
where
DDBS-
and DS-
are shorthand for anionic surfactants dodecylbenzene sulfonate and
dodecyl sulfate. Precipitation may also occur in solutions where
supramolecular aggregates known as micelles exist.
Micelles
limit the precipitation of ionic surfactants by acting somehow as
sequestering agents, and exist in solutions when there is enough
surfactant to exceed its characteristic Critical Micellization. They
are at the root of the unusual behavior of surfactants in solution,
and it will be shown in Supplementary Materials that ionic
surfactants are in fact a particular case of the general behavior of
sparingly soluble salts by demonstrating that their solubility
products can be linked to their surface excess.
It
was recently proposed that the CMC is just the bulk phase
concentration in equilibrium with a Critical Surface Excess of
Micellization (CSEM) [4].
When reaching CSEM, the distance between surfactant ions at the air
water interface the matches Bjerrum’s critical distance for ionic
pair formation. That the trigger condition for micellization is a
form of equilibrium reaction involving the surface excess of an ionic
species is at the root of the model to be proposed here. For example
[5]
N,N′-Phthaloyl-bis(2-aminododecanoic
acid) has a CMC of 1.8 10-6M,
and a CSEM of 1.71 10-6
mol m-2,
whereas NaDS [6]
at 33oC
has a CMC of 8.1 10-3M
but its CSEM is still 3.33 10-6
mol m-2.
Surface excess data at the CMC for many anionic, cationic and
zwitterionic surfactants gave values consistent
within 20% with Bjerrum’s distance, both above and below [4].
Therefore, in the case of surfactants an ionic pair-like assembly
like micelles, found across the solution, is linked to a
characteristic condition of its surface excess.
That
the equilibrium leading to a reaction (like the formation of the
complex or product “micelle”) is linked to a surface property and
not a bulk phase property does not need to be restricted to
surfactant. The solubility product of Fe(OH)3
is 2.79 10-39[1].
That means that precipitation will occur if there are more than 1.38
1014
molecules of Fe(OH)3
per litre of water. Or to put it in other form, if the volume per OH-
ion is a cube of less than 1340 nm of
edge, then precipitation will occur. It seems more reasonable to
assume that the reaction takes place between far higher
concentrations at the surface of the liquid and that the precipitate
is too persistent to redissolve if it becomes dispersed across the
solution.
When
Petersen and Saykally [7] confirmed the Jones-Ray effect (the
existence of a minimum in the surface tension of dilute solutions of
some electrolytes around a concentration 1mM), in their modelling
work they predicted the existence of separate anionic and cationic
surface and subsurface excesses in a solution. The layers themselves
are calculated to be several Å thick, with the cationic layer being
thicker than the anionic. The 13 Jones-Ray electrolytes investigated
include compounds like MgSO4,
KClO3,
NaCl, LaCl3
or K3FeCN6
The distribution can be regarded as two planes with average surface
charge densities proportional to the surface and subsurface excesses
of both the cationic and anionic layer (Figure 1). Such structure is
similar to the structure of the surface excess of monofunctional
ionic surfactants [8].
Figure
1. (left) Density profiles [1]
for the de-coupling of
cations and anions near the air water interface of a Ray-Jones
electrolyte in water. (right) Surface excess of an ionic surfactant
and opposing counter ion layer. Although dispersed as colloids,
surfactant micelles are also shrouded by counterions.
1.2.
Basics of a planar model for chemical reactions in a single solvent.
Three
ideas are central to the model proposed in this paper. First, that
saturation of the surface surrounding the volume of liquid may limit
the value of the surface excess G
and cause a drop in chemical activity when the chemistry of the
system depends strongly on G
and not on the bulk concentration. Second, that free ions or
reactant molecules, together with ionic pairs or product molecules
forming at the surface are shuttled by mechanical agitation to and
from the bulk phase, where they may remain stable or decompose due to
solvation (Figure 2). Third, that products or intermediates shuttled
back to the surface may experience ionic exchange reactions when they
resume contact with the high concentration surface or subsurface
planes.
The
basis of the model is that, for the systems for which this model is
relevant, irrespective of whether the surface excess is anionic [7]
or vice versa [9], the counterion concentrations peak at a certain
distance from each other. A likely explanation for the separate
planes is that one of the species is only slightly soluble and its
excess becomes pushed towards the boundaries of the solution by being
excluded from solvent clusters. If the other species is more soluble,
it may be dragged behind by the electrostatic attraction of the
first. This must be countered by diffusional forces within the
solution and its better solvation, which explains why it remains
apart of its less soluble counterion.
Figure 2. In a solution
of two counterions one of the species may become pushed towards the
boundaries of the solution by its sinability to solvate. The other
may then be drawn by the first through electrostatic attraction but
is also scattered due to turbulence in the solution, hence its more
spread distribution (fig 1). Transfer to the bulk of the solution may
result in decomposition of products creating the appearance of no
reaction. Absence of stirring causes the process to be extremely
slow.
As
the concentrations build up, the surface and subsurface excesses will
raise until the electrostatic forces between planes drag together the
ions and allow them to react. There are several possible outcomes of
this condition. The salt will always be soluble if the reaction
product fails to form due to the characteristics of the solvation
spheres of the ions [10-11] or if it dissociates when transferred to
the bulk of the solution due to strong tendency to solvate of at
least one of the ions.
A
salt will also be very soluble when the combined surface excesses of
both counterions make it hard to meet the condition for electrostatic
attraction. When both counterions have high surface excess to bulk
phase concentration ratios and their salt is stable, they will be
slightly soluble. Of course, while some salts may precipitate solely
at the surface/subsurface of the liquid, more soluble salts may start
precipitating there and then seed bulk phase precipitation. Any solid
formed anywhere in the solution could become the source of new
surface and therefore new surface excess, providing and an additional
chance to react. That would be the interpretation of crystal seeding
within this model.
A
saturation surface excess value for ionic surfactants [7] would be in
the order of magnitude of 3mmol
m-2
contained in a layer of significantly less than 5 nm. The
concentration would therefore be higher than 0.1M. A likely order of
magnitude of bulk phase. e.g. surfactant concentrations in
equilibrium with such values (e.g. a critical micellization
concentration) may be 10-3M
to 10-7M.
Such surface excesses are very similar to values around 1.25 mmol
m-2
found for cations of even highly soluble inorganic salts like NaClO4
as reported by Lopez-Perez et al [9]:. It is clear that reaction
(e.g. micellar assembly) in the bulk phase is less likely to happen
than reaction in the surface excess region.
Figure
3. Some simple calculations around the volume of a cube. Although the
volume occupied by the dilute bulk concentrations more than
compensates for the lower reaction rates, can species far apart
really react in the bulk of the solution? Or is it just happening in
the surface and subsurface excess regions within the peripheral
region around the volume?
1.3.
Refutation of a preliminary objection: irrelevance due to the low
molar ratio surface excess to bulk concentration.
The
proportion of chemicals involved in the surface reaction would almost
always be small. However, in chemical technology and engineering
mixing is used when preparing samples and in many reactors (“stirred
tank” type reactors and “plug flow” reactors under turbulent
mixing would be two typical cases [12]) and other devices. This
renews the contents of the liquid surface [13], and we will show that
it can be the surface of the liquid facing the reactor wall, not only
the air water interface. In fact, the surface excess is likely to
exist against any surface (e.g. a probe dipped into the solution or
the submersed outside of an injection or sampling device).
If
the relative concentrations in the surface/subsurface layers are
substantially higher than in the bulk phase, then the intermediate
region between the two peak regions becomes the volume where reaction
intermediaries and final products form, because the kinetics will be
much faster.
Figure
3 suggests that the distances between species in the bulk phase may
simply prevent any reaction to take place there. In such case, most
kinetic reactions are likely to include within their frequency factor
an element accounting for the rate of transfer between bulk phase and
interface under ideal mixing conditions.
2.
Model and Discussion
2.1.
Activity coefficients as a ratio between actual and expected surface
excesses.
For
the discussion in this section it is irrelevant whether the ideal
behavior of a solute is linear proportionality between surface excess
and bulk concentration or adherence to an ideal isotherm like
Langmuir's. In section 2.2 it is suggested that linear
proportionality should be regarded as the ideal behavior. We are
going to illustrate the idea that non ideality is linked to the
discrepancy between the actual surface excess and the projected value
based on the bulk phase concentration. The expression presented here
allows to estimate the evolution of the surface excess G
with the increase of the bulk phase concentration C of a species. Its
origin is described in detail in Supplementary Materials. The
expression relates the surface excess to the total concentration and
a threshold concentration at which a transition in the G-C
relationship occurs:
where
a, b
are constants expressing the G-C
transition and kC is the theoretical G.
The activity coefficient, according to the model presented here,
would be:
Note
that the value of k is irrelevant for the calculation of g.
For AgNO3 in Figure 3 (top), the parameters for the
prediction of the activity coefficient are:
C≤
9 10-4M g=1
C≤
1.05 10-1M CThreshold
= 9 10-4M
a=1
b=0.9
C≤
2.53 10-1M CThreshold
= 1.05 10-1M
a=0.9 b=0.3
C>
2.53 10-1M g=[2.53
10-1M]/C
The
values have been chosen manually, simply to demonstrate that a
progressive decrease in the ability of the solute to deploy
proportionally at the surface would explain the evolution of the
activity coefficient. The visual aid lines show the changes in slope
in the activity of AgNO3. The trend is consistent with a
final situation where G cannot
increase further but there is no change in the structural nature of
the surface excess.
For
the AgNO3 case, replacing the system above for a Langmuir
isotherm yields a smooth functional variation (not plotted), but
still gives a consistent trend for the evolution of the activity
coefficient. For CaCl2 in Figure 3 (bottom), the
parameters for the prediction of the activity coefficient are:
C≤
9 10-4M g=1
C≤
1.25 10-1M CThreshold
= 9 10-4M
a=1
b=0.9
C≤
2.07 10-1M CThreshold
= 1.25 10-1M
a=0.9 b=0.3
C>
2.07 10-1M CThreshold
= 2.07 10-1M
a=0.3 b=50
Figure 4. Mean activity
coefficients for AgNO3 and CaCl2, [10] and a
prediction based on an estimate of the ratio between effective
surface excess and theoretical surface excess.
In
the case of CaCl2
the prediction is less accurate, which is to be expected because the
model tries to adapt to a change in the nature of the surface of the
liquid. The parameters propose a superactive surface excess by means
of b = 50 above a certain threshold concentration. This may represent
the development of a ionic liquid-like nanolayer or a condition where
one of the species is replaced by an intermediate (e.g. an ionic
pair) and becomes more reactive. Activity coefficients at
concentration of 15 mol kg-1
like 33.8 for Pb(ClO4)2,
43.1 for CaCl2
or 323 for HClO4
[1] may be explained in this way.
2.2.
Beer's Law and surface excess across all the liquid surfaces.
We
are going to use colorimetric results to propose that the surface
excesses appear and must be accounted for against all limiting
surfaces including walls, and not the air-water interface or the
surface of an adsorbent. It is irrelevant if the surface excesses are
identical or not in all cases.
If
ideal activity relates to linearity between surface excess across all
the surfaces of the liquid and bulk concentration, then the
transmittance/concentration plots must actually be describing the
transition from linear to non-linear relationship between surface
excess and bulk phase concentration, and the region of compliance of
Beer's Law must match
the region where the
surface excess/bulk phase partition is linear.
Otherwise the model would be inconsistent with actual observations.
Within the region of compliance with Beer's Law [14] and linear
proportionality between bulk concentration and surface excess, total
and bulk concentrations and surface excess follow:
where
S is the surface and V the volume of the cell filled with a sample
of concentration C. The bulk concentration would relate to the total
concentration following:
As,
S/V decreases with an increase in the optical path length, for a
given total concentration the bulk phase concentration will increase
with the optical path length because less solute is required to
provide the surface excess. As a consequence a sufficient increase of
the optical path length would increase the surface excess of the
liquid until saturation. This is observed in the work by Yu et al
[15], where merely by enlarging the cell's optical path a non-Lambert
Beer region is reached. If we consider the total contribution to the
absorbance as made up by the contributions of the bulk phase and the
surface.
where
the first right hand term refers to the classically accepted
contribution by the bulk of the solution and the second right hand
term corresponds to the effect of the surface excess (monomolecular,
hence the lack of a thickness) at the entry and exit planes of the
cell we can see the relative drop in absorbance as shown in
figure 5.
The
“no saturation” plot combines equations 5 and 6, assuming CTOTAL
=1 and K = 1. The extinction coefficient is irrelevant as the plot is
for the ratio between the absorbance at a given optical path length
and that at 0.5 mm. The “saturation” plot assumes that at 2.25
mm, the surface excess G=kCBULK
becomes constant because the surface-volume ratio has already dropped
so much that the surface excess becomes constant. The “Langmuir
isotherm” line shows that using an isotherm instead of Equation 3
predicts an earlier drop in surface concentration and absorbance.
Within
the scope of this paper, this would confirm that when an adsorption
isotherm can be used to predict the dependence of surface excess with
bulk concentration the system would already be non-ideal. We
should keep in mind that the surface excess may be very dense.
Petersen and Saykally [7] proposed in their model that the anions of
the Ray-Jones electrolytes may constitute the whole of the solution
in the layer where their surface excess peaks, even with the nominal
concentration 0.001M relevant to the Ray-Jones behavior.
Therefore,
while molecules in the solution may be randomly oriented when hit by
a photon, part of the reason for high light absorption may be optimal
orientation of the molecules in the surface excess to capture
incoming photons, whereby there would be a bulk phase molar
extinction coefficient eBULK
and a surface excess extinction coefficient eSURFACE,
with eBULK
≠
eSURFACE.
This is illustrated by using equation 6 for a prediction, unadjusted
for surface saturation, but for which it is assumed that the eSURFACE
=
1.25 eBULK
for the surface excesses found above the optical length 1.25 mm.
That explains the change in slope at higher path lengths.
Figure 5. Relative absorbances from Yu et al, and from the model. The basic
assumption of a contribution due to surface excess is enough to
predict what would otherwise seem a drop in the extinction
coefficient of the substance. The prediction is enhanced assuming
saturation has been reached at the surface and the only increase in
absorbance is due to the bulk phase.
However,
within the region where Beer's Law holds, it will not be possible to
discriminate the impact of the surface excess except through changes
of the surface/volume ratio. This would be independent of whether the
system's light absorption is controlled by the surface excess, by the
bulk phase or a combination, because in all cases it would be a
linear function of CBULK.
The role of the chemical equilibrium in the solution is obviously
important to establish the importance of the surface excess. Buijs
and Maurice [16] provide absorbance values for solutions of Pu(IV) in
the presence of different concentrations of H2SO4.
At
their highest H2SO4
concentration (4M) , for cells of
length 1, 2, 5 and 10 cm, the absorbance ratios relative to the 10 cm
cell are 0.13, 0.25, 0.58 and 1, which are consistent with the
asymptotic increase in S/V to ∞
when the optical path length tends to 0. This is consistent with the
results by Yu et al. For other samples with lower concentrations of
H2SO4,
the absorbance ratio is more or less constant, suggesting that the
contribution of the surface excess is directly proportional to the
bulk phase concentration and that the model where the surface excess
plays a role and the classical approach cannot be discriminated.
It
should be mentioned that Buijs and Maurice describe some equations
for the prediction of deviations from Lambert-Beer 's Law based on
relationships between optical length, concentration and absorbance of
the form:
(7)
where
p,q,..,z are constants. Said equations for the deviation from ideal
behavior are similar to Taylor series for a Langmuir or similar
adsorption isotherm [17]. This is further evidence of the connection
between ideality as a consequence of linear dependence of surface
excess and concentration.
Having
shown that surface excess may have an influence on light absorption,
that divergences in absorbance from ideal behaviour may be explained
by saturation of the surface excess, and therefore that surface
excess should be regarding as playing a major role in the chemistry
of all surfaces of a liquid facing any other surface other than air,
we are going to discuss the consistency of the proposed plane
reaction model with existing equilibrium and kinetic equations.
2.3.
Mechanism for precipitation of sparingly soluble salts with formula
AB.
Let
us consider that sufficiently high surface charge densities sA+
and sB-
should generate enough electrostatic attraction to draw together
counter ions from their planes and form a precipitate AB. Let us
assume that the condition is similar to Bjerrum’s distance for
ionic pair association [18], and dependent on the charge densities of
the charged planes:
where
the bulk phase concentrations [A+] and [B-] would be proportional to
the surface excesses GA+
and GB-.
Such expression is consistent with the form of a solubility product.
The plane structure is shown in Figure 6 (bottom, left). It becomes
evident that any deviation from linearity, for example the inability
of G
to increase with bulk concentration due to surface/subsurface
saturation would reflect in activity coefficients different from 1.
Figure 6. The schematics show that it is possible to arrange a reaction path
as a sequence of steps caused by migration from the starting planes
into a prime intermediate plane where the first intermediate forms.
Whether the first intermediate migrates to subprime intermediate
planes or reacts with other species in the prime intermediate plane
is debatable, but the scheme explains the reaction sequence.
In
this particular A + B = AB case, it makes sense to assume that a
“prime intermediate” plane physically exist, where species A+ and
B- migrate due to electrostatic attraction to reach. With this
scheme, it makes sense that if any of the plane charge densities is
initially too low to match the critical distance, precipitation will
not occur. Precipitation will cease when both the A and B planes are
depleted until their inter-plane electrostatic attraction is too low.
The model also explains precipitation when two chemicals are present
in non-stoichimetric concentrations: the force of the electrostatic
attraction depends on the product of both surface charge densities.
2.4.
Precipitation of sparingly soluble salts AxBy
intermediate species planes.
For
a more complex molecule AB2
the precipitation could be explained by an initial drawing together
of A2+
and B-
to form AB+
in a “prime intermediate” plane. The new plane (Figure 3, center)
would be involved in the drawing together of AB+
+ B-
to form AB2.
AB+
will be present in this plane at a concentration (comparable to a
surface excess) dependent on the equilibrium GAB+=
KeqG*
AG*B,
where G*
denotes the “plane
excess” in A2+
and B-
in the AB+
“plane”.As a consequence the precipitation step to produce the
insoluble salt would require to meet the
condition:
Rearranging
9 it can be seen that the product [A2+][B-]2
is equal to a constant value under some conditions: independence of
Keq
from surface excesses and linearity between surface excess and bulk
phase concentration.
This
migration between species planes and subsequent species plane
generation would explain also any precipitates with more than one
cation or anion and multiple precipitation options depending of the
temperature and composition of the mixture, like alum (KAl(SO4)2)
shown in Figure 3(right) [19]. Depending on the specific conditions
of an experiment, either K2SO4,
Al2(SO4)3
or alum may be the less soluble species, and precipitate. Although
Figure 3 (right) does not show more detail, it is obvious that other
competing “plane” paths include KSO4-
+ K+
to give K2SO4
and SO42-
+ AlSO4+
to give Al(SO4)2-
followed possibly by AlSO4+
+ Al(SO4)2-
to give Al2(SO4)3.
A
multiplanar arrangement (beyond
three planes) would be a simplified
description of something more complex. If an species of charge
intermediate between the two original planes deploys between them,
then it will partially shield them and allow them to be more
separated from each other. That could allow
further planes to exist. Such evolution
would conform with the multi-plane idea. Alternatively, the
intermediate plane may become the site for all the intermediate
species and the locus for all the reactions
between the initial species and the final product. The
mathematical forms would be anyway equivalent.
Before
extending the analysis to other types of reactions, with equilibria
involving initial and final product concentrations, we will discuss
how the definition of mean activity coefficients fit with this model,
and also the way in which the nature of the surface/bulk partition
would cause it to be masked by photometric methods is discussed
below.
2.5.
Consistency between the model and the concept of mean activity
coefficient.
If
the meaning of the activity coefficient is the deviation between the
actual value of surface excess of a species and an ideal value of
surface excess linked to the actual bulk phase concentration and
following the equations presented in the previous sections we can
deduce the form of the mean activity coefficient of a substance as a
function of ion activity coefficients [18]
If
we consider the activity coefficients of species A+ and B-
as
(12)
and equal to one for as long as Gamma = k [X], but different of 1 if Gamma becomes constant (for example) then we can see that equation 8 becomes
For
equation 13 the inclusion of non-ideality creates the correction
factor gA+(gB-)
which can be made equal to (gmean)2.
It is easy to see the mechanistic justification for the expression of
the mean activity coefficient.
It
is important to stress the novelty of the concept of surface plane
mechanism and how it justifies the exponents for the concentrations.
Although action mass models have been used for long time, they do not
explain the exponents in the equations, but simply acknowledge them.
In fact, if thought is given to the idea of bulk phase reaction, the
form of a solubility condition should be a relationship involving
concentrations with exponent one, such that the critical value
indicated the minimal amount of either of them required to
electrostatically atract the other in order to reach the final stage
of the reaction sequence, implicitly accounting for availability for
any previous intermediate reaction stages.
2.6
Other equilibria.
If
we revisit Section 2.2, where we looked
at the ”plane
excesses“ at the “prime
intermediate” plane, the proposition was
that the intermediate plane excess was:
for
any individual species forming in the “prime intermediate” plane.
In the case of precipitation, the end result is a neutral species
which does not significantly affect the structure of the plane system
from an electrostatic point of view.
Figure 7. Scheme of the
various intermediate planes for a sequence where all the
intermediates and products remain soluble in their planes.
However,
for reactions like complexation, where the product may be a charged
species, the equilibrium condition does not need to be depletion
until the surface planes do not have enough charge to attract the
species. The condition may be simply repulsion between same-sign
adjacent planes (E.g. A+2
and AB+)
cancelling transfer between them. This would suppress the ability to
further reaction between incoming reactants from opposite sign planes
and eventually terminate transfer. If we consider the total distance
as dA/B
= dA/0
+ d0/B,
and we define the three critical distances for equilibrium (Figure 7,
top) in terms of their plane charges s
as:
and
then rearrange equation 15 we find that for a given salt with 1:1
stoichiometry, we obtain a dissociation equilibrium constant:
From
here, in the case of a mixture of salts with common electrolytes, the
left hand side of the equation provides the relationship between the
common electrolytes, whereas the second term remains a constant that
gives the restriction value of KAB.
It becomes trivial that a subsequent stage leading from species AB to
species AB2
involving distances d0/-,
d0/1
and d1/-
and characteristic parameters a0/1
and a1/-
would result in:
which
is easily combined with equation 16 to yield:
the
form of the various equilibria and the connection between exponents
and stoichiometric factors is therefore justified. If
we go back to equation 16 we can see that we can rearrange the
equation to have the general form:
This provides the equilibrium constant with a shape similar to an adsorption isotherm. This is a shape consistent with correction factors for non-ideality in solubility products derived from the Debye-Hűckel model [20]. The Debye-Huckel model does not consider surface effects, but nevertheless the isotherm equation form appears in a potential form in the corrective term for non-ideality [21]:
where QS is the concentration-based apparent solubility product, KS is the acitivity based solubility product, a and b are constants, B(T) is a function of temperature, G(T) a series in T to different exponents, and I the ionic strength of the solution. Although equation 18 relates the “isotherm” form to the logarithms of the solubility products, the Taylor series of (1-x)-1 and -log(1+x) are very similar, including consistence in the signs for the terms in X to a given power. This means that non-ideality in the solubility product still will reflect the form of an adsorption isotherm. Nortier et al. [21], further developing on previous models on precipitation in complex systems, stress the fact that the underlying chemical mechanisms are not well known and cause the need for elaborate methods to account for non-ideality.
A
recent paper [22] on an accurate model for binding of cations onto anionic
micelles by ionic pair formation showed that one obstacle for earlier
recognition of the basic chemical process being a complexation-like
reaction and not an adsorption is that the equilibrium constant and
the adsorption isotherm can be found to have an analog underlying
mathematical form. The fact that the approach presented here shows
the same mathematical form than existing corrections for bulk-phase
models suggests these are implicitly corrected to account for the
surface excess factor.
2.7.
Kinetics.
While
the above mathematical developments suggest that the plane model
would explain the form of many equilibrium equations in solution, it
seems possible to justify kinetic equations in the same way. Let us
start by postulating that equilibrium in a solution is achieved
because the surface behaves as a reactor while the bulk phase behaves
as a storage area and feed tank. The equilibrium between the species
would be achieved in the surface, and they would remain stable for as
long as they remain in the bulk. Once they re-enter the
surface-subsurface, high local concentrations may cause exchange of
product fragments and free fragments. That would explain equilibria
which are not completely displaced to products or reactants, as well
as recombination when adding a further reagent or for example, an
isotopic marker. Equilibrium in the context of this section refers to
the final state of the reaction, whether a balance between direct and
reverse reactions or full conversion.
If
we consider the total volume of the solution V equal to ndA,
where d
is the thickness of the surface-subsurface layer, A the surface of
the fluid phase and n the geometrical proportionality factor with the
volume, we can define the bulk phase concentrations of the various
species Ci
once equilibrium has been reached as:
The
overall or macroscopically perceived rate of such reactions could
depend on two factors. First, the rate of replacement of the liquid
at the surface-subsurface layer may equal the rate of reaction if the
actual reaction rate within the surface-subsurface layer is
instantaneous. The rate of reaction would be affected by the
stoichiometry of the equilibrium within the surface-subsurface layer
in the same way that the equilibrium constant:
We can relate the frequency factor in the kinetic equation to the renewal term A/(VtR) based on Higbie's surface renewal model [13], where tR would be the time required to replace the fraction of liquid within the surface layer and the k constants can be related to the activation energy in Arrhenius constant.
The
overall rate of reaction may also depend on the rate of the reaction
within the plane, if tR
is shorter than the time required for the reaction to reach
equilibrium. In such cases, there will be a progressive increase in
the concentration of products as successive re-entries of chemicals
take place. In all those cases, it is proposed that the products do
not dissociate in the bulk of the liquid: dissociation in the bulk
would be related to processes where the product is unstable and
overall the process would be considered as no-reaction.
In
chemical reactor engineering poor mixing areas are accounted for as
“dead regions”[12] in compartmented reactor models, where part of
the reactor volume is supposed to behave ideally, part of it is
supposed to be stagnant (“dead”) and some is assumed to be a
recirculating volume: reinterpreting “dead” regions as regions
that are disconnected from surface renewal and thus denied access to
a reactive surface region maintains consistency between the viewpoint
of the model and experimental observation.
Conclusions
A
fundamental flaw in science is the belief that succesive
approximations to a numerically congruent solution/prediction to a
problem are mechanistically approaching the real behaviour of the
system. Succesive patches on an erroneous initial hypothesis, like
bulk phase reaction vs surface reaction in a fully stirred solution,
will correct the predicted value and will be pseudo-justified a
posteriori by yield a final equation that provides an accurate
numerical solution by amalgamanting a number of equations which,
individually, do not predict the real behaviour of any of the steps
or sub-processes of the system investigated. However, they will
return the same numerical value than the correct and unkonw aggregate
of functions. As a consequence, the real mechanims may be hidden
until a sufficient range of contradicting experimental systems are
found. However, the fundamental form of the real process may be found
by careful analysis of the empirically aproximated forms, providing
alternative sets of equations and asking what their physicochemical
meaining could be. In the final analysis, this paper shows that a sustained preconception, even when it affects a system which can be easily controlled, may affect the understanding of a physical phenomenon. As a consequence, it hints at an even greater chance for error in the understanding of systems which are not controlled or contained, as those dealt with by high energy physicists or astrophysicists.
Supporting
Materials. Precipitation of Ionic Surfactants: a surface reaction.
In
this Supplement we are going to show that the decrease of the
chemical activity of ionic surfactants as their surface excess
increases can be linked to a progression of their aggregation from
true monomers to two or three ion aggregates. This impacts on the
solubility of the surfactants. The form of equations 1 and 2 is
justified in this way.
Resistance
of the surfactant to precipitation beings before micelles form.
Figure 7 (bottom), closely inspired on work by Somasundaran et al
[23],
shows a generic logarithmic plot counterion concentration-surfactant
concentration showing the precipitation phase boundary. On this
figure, already below the CMC there is a region where the
concentration of counterion required for precipitation increases from
the linear precipitation region, and therefore resistance to
precipitation is already increasing. The surface area of
surfactants can be estimated from their surface excess at a saturated
interface (CMC or CSEM).
Any
transitions in aggregation below saturation would be unobservable for
a pure surfactant, and in mixed surfactant systems the norm is to
estimate an average surface area per surfactant head, as it is hard
to elucidate interaction between surfactant molecules and ions.
However, occasionally there are some systems which can provide more
information. We will show that there is a change in activity linked
to ionic surfactant pair formation at the surface of the liquid which
can be linked with increased resistance to precipitation. The
resulting expression is then used in the main text to justify that
chemical activity is linked to surface excess generally, and not only
in the case of surfactants.
Figure 9 shows two datasets by Gosh and Moulik [24], plus some visual aid
lines and correlation results. A series designated as Tween/DS
corresponds to a mixture of an anionic monovalent surfactant sodium
dodecylsulfate (SDS) present in solution as DS (dodecylsulfate) ions
and a nonionic surfactant molecule. The peculiarity of the data is
that it agrees with a linear relationship:
0.58
+ 3.91 XDS with
R2 =
0.9594. (23)
Figure 8. Schematic views of solubility contours of ionic surfactants. (top)
Residual surfactant concentration v total surfactant concentration
for a given counterion concentration. (bottom) Solubility boundary.
The
value 0.58 is the area of the head of the non-ionic surfactant Tween,
in nm2. 3.91 is the area of the head of ionic surfactant
DS, which is odd because for pure DS in a saturated surface excess
the same authors find the value 1.07. That is, DS is more compact
when found at the condition where Bjerrum critical distance is
reached (and therefore where it is found forming ionic pairs) than
when it is very diluted in a nonionic surfactant which does not
interact with it (hence the linear relationship).Figure 9 shows
equation 21 as a dashed line and the data for Tween. It also shows a
line broken in four segments corresponding to the calculation of
average head surface for the Brij/SDS system. The leftmost is related
to:
Molecular
Surface area = 0.79XBrij+3.93XSDS (24)
for
XSDS < 0.045
where
0.79 nm2 is the area of a head of surfactant Brij, 3.93
nm2 is the estimate for truly monomeric SDS ions at the surface of
the liquid when highly diluted in a non-interacting nonionic
compound, and 0.045 is a value of XSDS for which the
intersection with the lowest visual aid curve is found.
Figure 9. Experimentally
estimated and calculated average head surface area of mixtures of
ionic surfactant SDS and nonionic surfactants Tween and Brij. The two
straight lines linking the series of two and three open square points
are visual aids.
The
equation therefore describes the region where the surface area of
ionic SDS per head of ion is constant. The small segment of the
Brij/DS broken line, second from the right, that connects the two
visual aid lines corresponds to:
Molecular
Surface area = 00.79XBrij+1.9XSDS (25)
for
0.146<XSDS < 0.164
where
1.9 is a value attributed to an intermediate state, which is assumed
to be M+n(DS)2,
between truly monomeric DS and DS forming ionic pairs M+n(DS)3
or M+n(DS)4 as found in previous work on
binding of counterions onto DS micelles.
The
segments discussed can be explained away has being the consequence of
a critical condition having been met which causes DS ions to be in a
given state, and incidentally with a certain activity, which is
uniform over a range of concentrations. However, the segments second
from the left and rightmost require to be explained the respective
expressions
and
In equation 24 the contribution of the ionic surfactant in its true monomeric form with surface area 3.9 and of the first intermediate ionic pair with surface area 1.9 are weighed liearly over the range XDS 0.045 (the pair 1.9 appears) and 0.146 (the pair 1.9 is the only form).
In
equation 25, we consider the range XDS to be from 0.164 to
0.3 and the surface 1.33. There are no further data to the right
except for XDS = 1 where the surface area per head of DS
is 1.07 nm2, but the XDS = 0.3 provides a
reasonable fit with the surface area 1.33. The value 1.33 nm2
is picked as the area per head of a M+n(DS)3
because it seems a reasonable progression from about 4 nm2
for a truly free monomer to about 2 for each of the supposed 2
monomers more closely packed in a M+n(DS)2
group and on to about 1 (1.07 nm2)
for the highest stoichiometry M+n(DS)4.
Having
shown that the average surface per head of surfactant can be
calculated on the basis of a constant contribution of the nonionic
surfactant and a contribution of the ionic surfactant that varies as
its partial surface excess raises, we plot the partial surface excess
of the ionic surfactant (triangles) together with the solubility
curve for its insoluble calcium salt [25] in Figure 9. The open
triangles correspond to the partial surface excesses of DS at the
transition points of its various surface areas. The plot has a
similar shape to Figure 8 (bottom). Four arrows are depicted to show
there is a change in slope in the solubility curve, which can be
linked to the transition surface excesses. The surface excess which
would correspond to the transition from 1.33 to 1.07 falls short, but
it is an speculative value, and also at higher molar fractions of DS
the difference between micellar molar fraction and surface excess
molar fraction would increase. The conclusion is that the evolution
of the resistance to precipitation and therefore of chemical
acitivity is linked with a change in ionic structure at the surface.
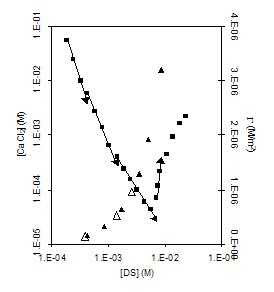
Figure 10. Plotting
surface excesses and solubilities of Ca(DS)2 against bulk
phase concentration of DS. Particularly at low concentrations there
is a surprising consistency between predicted transition points in
ionic pairing and transitions in solubility. The vertical dotted
line indicates the onset of micellization and of more complex
colloidal interactions.
We
will demonstrate now the physiochemical foundation for the equation
system used in the main text. With the three leftmost points, we
obtain an empirical correlation:
[Ca2+][DS]3.0604=2.0811
10-13 R2=1 (28)
The
equation is peculiar because the insoluble compound is obviously
CaDS2. The result has
been carefully double checked having extracted the data from the
original figure and used the pixel scale of a graphic package to
obtain from the lengths of the X,Y scales and the positions of the
points the actual values with high precision. A possible explanation
is that the precipitation of CaDS2
requires to go through an intermediate ionic group like
Na+[Ca2+(DS-)3]-
which would form at the interface, where the local concentrations
will always be higher, and decompose in the bulk phase due to the
lower local ionic strength. The slight difference between the
exponent and 3 can be just accumulated experimental error.
Irrespective of the reason for the form of the correlation, if we
attribute to Ca2+
a constant g
= 1 through the range of concentrations and to DS a value of g
= 1 only in this first series, we can estimate the activity
coefficient for DS in the other points of the plot as:
gDS
= (2.0811 10-13/[Ca2+])1/3.0605 (29)
For
the three series considered non ideal (the three rightmost arrows in
Figure 10), we proceed to calculate an estimated activity coefficient
based on the following scheme:
- gTB = 1 is chosen from the last ideal point as Threshold Base activity coefficient. The corresponding concentration is chosen as Threshold Concentration CThreshold.
- A seed gGG value is chosen for the last point of a linear segment as Goal activity coefficient, with the concentration there becoming the Goal concentration CG. It will be iterated to find the actual value of gGG in the equation
- gC = gTB Cthreshold/CG + gG (CG - Cthreshold)/CG, (30)
which
will provide the values for all the concentrations between the
Threshold and the Goal points, assuming that those two values are the
activity coefficients of the only co-existing ionic states in the
segment.
- For the next segment gTB = gG, and the process re-starts.
Figure
11 shows the comparison between the estimates obtained from Equation
27 and the predictive calculations. The increasing divergency for
lower activities reflects formation of surfactant micelles and
further non-ideality inducing factors. Therefore, the concept of
critical conditions causing a fundamental change in the
characteristics of an ionic species (ionic pairs, ionic liquid
layers) pre-existing condition and an emerging condition which will
become predominant provides results that are consistent with
observation.
Figure 11.Model activity
coefficients compared with activity coefficients estimated from the
experimental solubility curves. The results confirm the model
proposed in equations 1 and 2.
Keywords:
((surface excess · chemical activity · equilibrium constant ·
concentration plane · Lambert-Beer's Law))
[1] Handbook
of Chemistry and Physics, Lide, D.R., Editor, 86th
Edition, CRC, 2005
Boca Raton (USA)
[2] Somasundaran,
P.; Celik, M.; Goyal, A.; Manev, E. Soc.
Petrol. Eng. J. 1984,
April,
233-239
[3] Božić,
J.; Krznarić, I.; Kallay, N. Colloid &
Polymer Sci. 1979,
257,
201-205
[4] Talens-Aleson,
F.I. Langmuir.
2010,
26(22),
16812-16817
[5] Müller,
P.; E. Weber, E.; Helbig, C.; Baldauf, H. J.
Surfactants Deterg, 2001,
4(4) 407-414
[6] Lu,
J-R.; Marrocco, A.; Su, T-J.; Thomas, R.K.; Penfold, J. J.
Coll. Interf. Sci, 1993,
158,
303-316
[7] Petersen,
P. B.; Saykally, R. J. J. Am. Chem. Soc.
2005,
127(44),
15446-15452
[8] Zhao,J.;
Liu, J.; Jiang. R. Colloids and
Surfaces A: Physicochem. Eng. Aspects
2009, 350,
141–146
[9] Lopez-Perez,
G.; Gonzalez-Arjona, D., Molero, M., Andreu, R. Langmuir
1999,
15,
4892-4897
[10] Collins,
K.D.; Methods
2004,
34,
4300-311
[11] Hribar,
B.; Southall, N.T.; Vlachy, V.; Dill, K.A. JACS
2002,
124,
12302-12311
[12] Levenspiel,
O., Chemical Reactor Engineering , John Wiley & Sons, Inc 1999,
283-288
[13] Taylor,
R.; Krishna, R. Multicomponent
Mass Transfer
John Wiley & Sons, Inc. 1992,
220-227
[14] Brown,
C.W. Ultraviolet,
Visible, Near Infrared Spectrophotometers,
in Ewing's Analytical Instrumentation Handbook, CRC 2005,
127-139 Boca Raton (USA)
[15] Haiyan,
Y.; Xiaoying. N.; Bobin, L.; Yibin, Y.
Effect of Optical Path Length on Prediction Precision of Calibration
Models Developed for Enological Parameters of Rice Wine,
ASABE Annual International Meeting, Rhode Island Convention Center,
Providence, Rhode Island, June 29 – July 2, 2008
[16] Buijs,
K.; Maurice, M.J. Analytica
Chimica Acta
1969,
47,
469-474
[17] Spiegel,
M.R. Manual
de Formulas y Tablas Matematicas,
(Spa. Trans.) McGraw-Hill Mexico, 1970
[18] Levin,
I.N., Fisicoquimica
(Spa. Trans.) McGraw-Hill Latinoamericana S.A., 1981
[19] Christov,
C. Calphad,
2002,
26(1),
85-94
Mukerjee,
P.; Mysels, K.J. Critical Micelle
Concentration of aqueous surfactant systems.
National Bureau for Standards: Washington (USA), 1971
[20] Daune,
M. Molecular Biophysics: Structures in
motion.
(Eng.Trans) Oxford University Press 1999
[21] Nortier,
P.; Chagnon, P.; Lewis, A.E. Chem. Eng
Sci 2011
66,
2596–2605
[22] Talens-Alesson,
F.I. J. Phys. Chem. B.
2009, 113,
9779-9785
[23] Somasundaran,
S.; Ananthapadmanabhan, K.P.; Celik, M.S.; Manve, E.D. Soc
Petrol Engineers J 1984,
December,
667-675
[24] Ghosh,
S.; Moulik, S. P. J Colloid Interface
Sci. 1998,
208,
357–366
[25] Stellner,
K.V.; Scamehorn, J.F. Langmuir.
1989, 5,
70-77