Solubility in the bulk phase?
For
AlPO4,
the solubility product Ksp
equals 9.84 10-21.
Apparently, it is not possible for around 10-10
mol of such salt to be dissolved in 55 mol of water. This means that
up to 6 1013
molecules of salt can be dissolved in 3.3 1025
molecules of water. This means that a single molecule would break up
and saturate the volume occupied by 0.5 1012
molecules of water. When the aluminum cation and the phosphate anion
are each surrounded by a pack of one million molecules of water, then
the surrounding 499,998 packs of one million molecules of water would
be unable to hold a single aluminum or phosphate ions. It is hard to
believe that a bulk phase model can explain this system. We can take
it as an(other) exception to the general principles of chemistry, or
we can assume that it tells us something is wrong.
On
the other hand, let us consider a cube with a 10 cm edge. Yes,
containing one liter of water and 6 1013
molecules of aluminum phosphate. The surface of the cube is 600 cm2,
or 6 1018Å2.
Let us assume that formation of ionic pairs Al:PO4
against the competition of solvation at the surface of the liquid
decides whether precipitation occurs or not. Are the cations and
anions within range of each other for ionic pairs to form? If we use
Bjerrum correlation for the critical distance for ionic pair
formation (it is a bulk phase equation, so it could still be biased,
but lets go for it) we obtain a critical distance of 32.13Å at 25C
(the distance would be 3.57 ∙│+3│∙│-3│). The surface
controlled by every ion would be that value to the square, around
1000. And there would be two ions to the molecule, giving a total
“area coverage” of 1000 ∙ 2 ∙ 6 1013
= 1.2 1017
Å2.
It
still falls short by an area factor of 50 or a distance factor of 7,
but it seems less of an act of faith to rationalize this discrepancy,
particularly having considered the ions dimensionless. For example,
if a shorter inter ion distance does not allow for solvation spheres
to remain efficiently formed between phosphate and Al3+
ions, then this would
explain why the total concentration required to reach the solubility
product does not need to comply the Bjerrum correlation even if all
of it is at the surface. Or maybe the model can still be wrong. But
the feeling that the balance of probabilities might be in favor of
something closer to the surface excess model than to the astronomical
numbers of the bulk phase model is still there.
A
plausible alternative: surface excess model for the solubility of a
salt.
Let
us assume that the first requirement for a salt to reach saturation
is that, if present as a solid, the rate at which its ions will react
with a solvent and becoming solvated and breaking away is balanced
with the rate at which its surface excess will cause precipitation.
Let us assume that it will precipitate wherever a sufficient surface
excess happens anywhere in the solution, included the surface of any
solid salt present. Notice this does not necessarily mean the air
water surface: could mean any surface, like that of seeding particles
or already formed crystals. Or a pipe wall or a membrane/filter. It
is reasonable to assume that the surface excesses for each counter
ion in a salt will be on average deployed at different distances of
the surface as the solvation number will be different for both ions.
Some research on the Ray-Jones effect ,a minimum in the variation of
surface tension with the concentration of certain electrolytes at a
concentration 1mM (Petersen and Saykally, 2005) suggests such offset
would be part of the explanation of the effect.
In
practice, it could be looked at as some sort of parallel surface
excess planes containing each of the electrolytes (below) . Of
course, the molecules and ions in this surface layer will be renewed
by agitation, which is nearly omnipresent in chemical
experimentation. This may also have an effect on which counterion is
rejected faster by the solution by denying to it solvation water (or
the relevant solvent in the case of a non-aqueous system).
Anions and cations circulate due to agitation between the bulk phase and the surface and back. If the associations are only stable in the high concentration surface region, they will dissociate, but why should they otherwise?
This
model depends on the electrostatic attraction between the ions
overcoming the separation between the planes containing the surface
excesses (below) for reaction to occur.
The density of particles increases the electrostatic attraction: the difference between attraction (left) and complete separation (right).
When the surface excesses reach certain
values and raise the surface plane “charge density” ,
then some of the ions may migrate towards each other and form ionic
pairs of lower net charge. This may reduce the electrostatic
attraction between the surface planes to the point that the migration
does not happen any more and there is no reaction. This may have
resulted in precipitation, or merely in the formation of an
intermediate soluble species. The products and unreacted reagents
migrate to the bulk phase due to surface renewal caused by agitation.
There they would remain in whatever state they acquired at the
surface until they re-enter the surface excess region. Because, if an
ionic pair forms, why should it break up in a diluted solution. where
the solvent could not prevent the pairing in the first place? And if
it breaks up, because it was only the local high concentrations that
drove it to form, why should it reform in the bulk of the liquid?
Of
course, we know that some state of flux between species exists in
solution. But this could be explained simply by a competition between
surface excess components to exchange with a component of a
particular ionic pair as it re-enters the surface excess region, and
not a bulk-phase phenomenon (below).
”a” represents a kind of ions present in one of the surface excesses, “b” represent the counter ion present in the other. The figure shows how an already formed aggregate, present in the bulk phase, may re-enter the surface region and exchange part of its components.
How we would notice the
difference? The surface excess would be up front the sensor, unlike
the bulk phase concentration. If the condition for precipitation is
that a given electrostatic attraction pulls together the ions on both
concentration planes, this is actually independent of the individual
superficial concentrations, and only depends on the product of the
surface charges reaching a given value. This formally explains the
solubility product of a salt: different values of surface charge
density at both planes can yield the same electrostatic attraction,
required for the reaction to take place. This can be seen as a
product of concentrations, because the surface excess is a function
of the bulk phase concentration (below). The detailed discussion, expanded to
equilibrium constants and kinetic equations can be found in
The Weierstrass Snare post.
If the attraction is electrostatic, it is irrelevant whether the charge density is contributed by one or the other of the ions suitable to cause the reaction.
Objection
to an accepted truth: A bulk phase solubility condition without
cheats.
The
main difference between a bulk concentration and a surface excess
model is the absence of a singularity: the condition must be met
throughout the solution. We still should assume that ionic pairs must
form as preliminary or be a trigger condition for precipitation.
Therefore, that some form of critical distance between counterions
must exist, even if it is not Bjerrum's. Extremely low solubility
products, which can never be explained with final concentration links
to ionic pair distances, will be dispenses with considering that
their existence as precipitates is a consequence of the initial
stages of mixing: after all Al(OH)3
may precipitate with different forms and very different solubility
products, purely as a consequence of mixing conditions. Therefore,
the condition may have been met during the mixing and almost no
precipitable materials “survived” the mixing. This is already a
concession, as in fact these extremely low solubility compounds would
be against the bulk-phase mechanism because their justification would
be a transient mixing condition.
There
are a number of problems. The model assumes homogeneous mixing. Let
us say that the target precipitate is AB2.
A+2n
is present in a given concentration. B-n
is added. There is no real reason for any AB2
molecules to come apart in the bulk of the liquid if it has formed
there. Remember, what we see may deceive us. We have already given a
surface excess alternative to dynamic exchange or reconfiguration in
solution. Just because high energy, fast moving molecules in a gas
mixture may experience collisions between them and with the walls and
change there (the equilibria in the synthesis of ammonia or sulfur
trioxide, for example) does not mean that slow, shielded (solvated),
low energy ions in solution should behave in the same way.
The
possibility of AB2
to form before all A+2n
as reacted to form AB+n
could depend on the mixing conditions. As solubility products are
constant and generally do not do this, we must assume that AB2
only forms when AB+n
has formed in sufficient amount. We should remember that we should
let the models predict dynamic equilibrium and the mathematical form
of solubility products without our help. If a compound in a diluted
solution forms in the bulk of the solution, there is no reason for it
to decompose and reform continually. If we assume that any ion-ion
interaction depends of a characteristic distance to happen (below) then we can develop a set of equation to describe the process.
If there is such characteristic distance for the interaction of A and B, then interaction will occur whenever the whole volume of the solution is encompassed by the two ions:
If there is such characteristic distance for the interaction of A and B, then interaction will occur whenever the whole volume of the solution is encompassed by the two ions:
A
+ B
must be equal to 1 for the solubility condition to be reached. If
this is the case, then the trivial development for the precipitation
equation is:
The
relationship for a solubility condition clearly goes in the lines of
one rises the other lowers, but it is not mathematically equivalent
to a solubility product. If the sequence is not A+B equal AB, but A
+2B equal AB2,
then there would be a subsequent condition
It
is hard to see how these equations have any connection with
conventional solubility products. So, the fact is that following a
rationalist approach, instead of an empiricist one allowing for a
mixture of empirical facts and axioms, bulk phase solubilities do not
look like the real thing, while surface tension-related solubilities
do.
References.
Petersen, P.B., Saykally, R.J., Adsorption of Ions to the Surface of Dilute Electrolyte Solutions: The Jones-Ray Effect Revisited J. AM. CHEM. SOC. 127(44), 15446-15452 (2005)F. Talens-Alesson (2011) http://chemistry-f-talens-alesson.blogspot.co.uk/2011/09/some-g-g-and-d-symbols-in-text-must-be.html








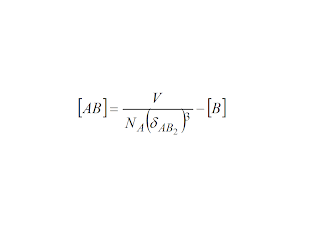
We make the custom synthesis process more efficient and cost effective while maintaining the highest standards of quality and reliability. 1-octyl-3-methylimidazolium perchlorate
ReplyDelete