Surface Tension in Liquids: the structure and properties of the tension layer

© 2013 Federico I. Talens-Alesson

This manuscript discusses the idea that the boundary layer of liquid, where surface tension manifests itself, has an impact on a range of phenomena occurring in solution. It does it by being a region of singular viscosity and density compared with the bulk of the liquid. As such, it is the packing of molecules of solvent near the surface of the liquid influences the occurrence of surface excesses of solutes. Other phenomena are also described.

It is accepted that intermolecular forces in a liquid reach a singularity at the boundaries of the liquid with gas and solid phases. The molecules at the surface are pulled inwards in because there are no “outward” pulling forces. That creates the phenomenon of surface tension.

It is known that under certain conditions some liquids deposit layers on vertical or even upside down surfaces, continuous and well above the surface of their main surface, in a phenomenon linked to capillarity. Such liquids are called “super creepers”  and there is a maximum thickness to their layers coating surfaces higher than the surface of the liquid itself.

 There are many interesting questions about how this surface tension works. Amongst these, one is how surface tension modifiers work, and another is how surface tension plays a role in heat and mass transfer in multiphase flow.


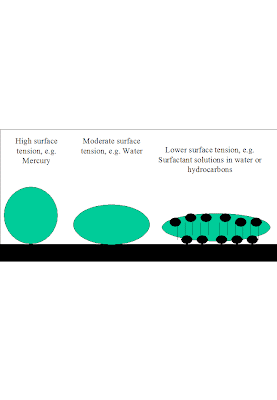
Surface Tension and Surfactants.

Surface tension is seen as a force that “tenses” the surface of a liquid. The higher the surface tension the more difficult it is to ripple the surface. This is a relevant technological question, as ripples (or waves) on the surface of a liquid have an impact on phenomena like the ability of a gas-liquid absorption device to perform, or the ability of a heat exchange device to perform, because in some cases such devices consist in pipes with liquid  circulating along their walls “pushed” by a core of gas streaming through the center of the pipe. The ripples play a part on how much mechanical energy is transferred from the gas to the liquid to facilitate the latter's circulation. The “surface tensing” is also observed in the fact that, the higher the surface tension, the rounder will be the drops of liquid on a solid surface. Reducing the surface tension to flatten drops of liquids on solids and increase contact angles is part of wetting and detergent technologies, for example.

Surface tension modifiers, known as surfactants, have a number of characteristics, including the fact that they have a hydrophobic and hydrophilic fragment. Or several from one of the kinds, or from both. Surfactants require a minimum length of their hydrocarbon chain to be so. In aqueous solutions, they lower the surface tension. Sodium butyl sulfate is not a surfactant, sodium dodecyl sulfate is. A peculiarity of the drop in surface tension induced by surfactants is that it does not lead to an straightforward increase in “rippleness” in the liquid surface. A re-tensing effect called the Marangoni effect causes ripples to be flattened out more in a surfactant solution than in a pure liquid which had the same surface tension by its intrinsic properties. Surfactants are considered to insert their polar heads into aqueous solution, and keep the hydrophobic tails above, giving the solution the “hydrocarbon” surface tension.

Alternative View on Surfactants and Surface Tension.

If you have read any of my previous blogs, you will not be surprised to find that I disagree and have an alternative view about the thing works.

Children often play chase games, where one of them has to chase other children. In a variant, the chaser and the first chased join hands and then proceed to chase another child. As the chain grows longer, the centre of the line, which moves abreast to cover more field, is tensed with the children's arms stretched out. However, the children at both ends of the line are invariably pulled inwards the centre of the line. The actual way the mechanism causing surface tension should be looked at in this way: molecules vibrate, and when their vibration is away from a certain molecule they have an attractive force with, they yank it. If they move TOWARDS it, nothing happens but it is guaranteed that when it moves away it will yank the second molecule HARDER. This causes a chain reaction, which combines with other similar “pulls” by other molecules in all directions. The result should be that when there are molecules at long distances in all directions (well, from a molecular point of view), the matrix of the solution should be greatly expanded. When the phenomenon takes place closer to a surface, then the “pull” from that direction is reduced, until it decreases at the surface itself. As a consequence, molecules near a surface would be more tightly packed. By the way, this implies that the liquid near the surface is actually denser and, insofar as the viscosity of a solution or liquid is a consequence of the strength of the intermolecular interactions and the number of interactions per unit of volume (as a consequence of the density of molecules),  more viscid than in the core of the solution.

A possible explanation of super creeping is that the wall does not provide enough energy to “kick out” the molecules depositing on it. The fact that a critical thickness exists would be related to an increase of the intermolecular interactions and the “loosening” of the liquid layer, leading to molecules sliding down the surface of the film. This critical thickness layer hints to a surface tension layer. The surface tension layer would be the layer near the boundary of a liquid or solution where the molecules are more tightly packed and create the surface tension phenomenon. The super creeper liquid film would be a limiting case in which any surface, due to the low energy of the system, could contain a surface tension layer before any excess just slid down because the binding becomes too loose.

I propose that, instead of the usual view, the surfactant molecule is sunk into the liquid as a buoy, polar head inwards, with maybe the final fragment of hydrocarbon chain sticking out. The hydrocarbon chains of surfactants would interfere in a way similar to graphite rods in a nuclear reactor: instead of interfering with the “line of sight” of fissile nuclei “firing” neutrons at each other, they interfere the attractive interactions between the molecules. As their hydrocarbon fragments replace strong water-water interactions with weaker interactions with the surrounding liquid molecules, they “loosen” the surface tension layer, which leads to a loosened “wrapping” of the bulk of the liquid and increased surface to volume ratio. In three dimensions, it would not simply result in the hedges being pushes inwards, but in a more compact three-dimensional structure progressively loosening from the surface to a certain critical distance.

Marangoni Effect.

An explanation for the Marangoni effect follows easily from the above description: when a ripple breaks the surface and causes liquid from the isotropic bulk to surface, the balance of forces within the new surface must be re-established due to the new anisotropic conditions. That implies a densification of the surface liquid in the “gash” which somehow begins to “knit itself” together and as a consequence the hedges of the “gash” are pulled together. This approach is sufficiently similar to the regular approach to be indistinguishable, although it is the complete opposite: the “pull” is a consequence of the “bare bulk” liquid NOT being densified already and having to build up the surface tension. These build-ups are the ones causing the Marangoni effect. But it looks the same as assuming that the “bare bulk” region is a high surface tension area already, which is the conventional view.

Solubility Implications of the Existence of the Surface Tension Layer.

A densification of a polar solvent like water near the surface leads to further proximity between polar groups from solvent molecules. If we consider an electrolyte breaking up during dissolution in a polar solvent, with an anion recognized by current knowledge as having near zero hydration number, and a cation recognized as having 3,4 or whatever hydration number, what we know is that one of them has no tendency to associate with water molecules (for example) and the other does. But there is an issue there. If the anion really cannot hold onto solvent molecules, then it can migrate all the way to the surface and create a surface excess of itself. If the cation has an optimum number of “held” solvent molecules, it will have an optimum deployment place where the attractive forces of the anion surface excess and the polar solvent, and the repulsive charge of the transient bulk excess cation concentration balance. Therefore, the cation will have some form of subsurface excess, because it will be pulled away for the surface of the liquid by the solute-solvent interactions. This actually connects seamlessly with my reaction surface planets theory, and gives an explanation to why there would be separate surface excesses for anionic and cationic species.

In the case of a salt AnBm, which dissociates in A+m and B-n ions, the initial surface excesses would be one containing B-n likely to have near zero hydration number and be right at the surface of the liquid, by reason of nothing pulling it back into the solution. The cation A+m will have a tendency to be associated to solvent molecules, and it will create its surface excess at some distance of the surface. However, as the concentrations increase, the electrostatic pull between the two surface excesses causes some ions to meet at an intermediate point, forming ionic pairs AB(+m-n).

These pairs will have their own optimum solvent-interaction characteristics, and therefore their own hydration number and distance from the surface at which to build their own surface excess concentration. This surface excess shields the other two, because it is same charge than one and has a lower to interact with the other. Also, its appearance may have caused some depletion in the other surface excesses. If its distance to the opposite charge surface excess is too large to cause a subsequent step, then the reaction stops there. This explains why in an equilibrium with many species not all of them are present at all times. The reader is referred to the other document to see what the connection between this surface excess layer structure causes the know mathematical definitions for solubility, equilibrium and kinetic equations.

Summarizing, the surface tension layer creates a net which filters the various types of ions, creating a restriction to the relative deployment of the various surface and subsurface excesses versus the actual liquid surface. The solvent density at each subsurface excess plane is not the same, and this brings an interesting question: if the hydration number refers to an optimum value at the surface excess plane, there is no real reason for the value to be the same across the volume of the solution. Also, because even when we use probes we can only sense or measure at the surface of the solution, what we get is a distorted combination of the closer signal from the surface excess and the more distant signal from the bulk phase, which is nevertheless weaker and more diluted. Therefore, sensing indicating a given hydration number could refer mainly to surface excess hydration number, that nevertheless would be the relevant one, as reactions would take place at the surface/subsurface layer level.


Precipitation, Nucleation and Crystal Growth.

An immediate idea is that when precipitation takes place, then any crystals forming would contribute new surface against which surface and subsurface excesses can build up. In fact, the process by which new crystals form (nucleation) should also take place in the surface excess regions. Therefore any air-water interface (e.g bubbles), any liquid-liquid surfaces and any solid -liquid surfaces could cause nucleation (for example, by seeding). Even crystal growth would be a combination of direct assembly of ions onto the surface of a crystal (well formed crystal growth) or nucleation adjacent to the surface of an existing crystal (imperfect crystal growth).

Better structural matches between forming ionic groups and available surfaces would result in higher crystal growth rates and better quality crystalline structures. This is observed in surface coatings, where different chemical compositions of coating baths may lead to a range of amorphous or micro-crystalline coatings.

As a collateral finding, the existence of extended surface (dispersed particles of whatever kind) means that the proportion of liquid in surface tension layers increases and therefore the average density and viscosity of the liquid fraction of a dispersion/ suspension would already increase, irrespective of the impact of the intrinsic contribution of the dispersed fraction. Finely divided materials with higher surface/volume ratios should contribute more strongly to viscosity increases than more coarse particles to “static” viscosity.

While the increase in density is directly connected with the number of particles per unit of volume, the strength in the interactions between molecules causing viscosity will depend on a potential law of the distance and a function accounting for the number of interactions. The inverse square of the distance of interaction is:

(4π/3 ρ)^(2/3) = 1/r^2 α Fintermolecular interaction

where r = n/V is the particle density and the number of interactions between the n particles in a volume unit V is:

leading to a “energy per unit of volume and unit of time”(dimensions of dynamic viscosity) proportional to a function of the form:

This function shows that there is a link between increase in density and viscosity for a given liquid by the mere presence of an interface or boundary. The meaning would be the energy used up to generate the “pull around” required in a moving fluid: larger values for more viscid liquids, smaller values for less viscid liquids.

Let us go back to the question of suspensions of particles. Let us assume that the effective (average) viscosity has a proportionality to the viscosities and volume fractions of the bulk phase and tension layers. Let's assume that the average viscosity of the liquid in a dispersion can be considered an average of the bulk phase and tension layer viscosities. This is in conflict with the forms of viscosity equations for mixtures of substances, but it leads to an interesting result. Follow me.

where V is the volume of the liquid, and VB and VTL are the volumes of the bulk region and the tension layer:

The volume does not specifically includes the volume of the materials dispersed, but it takes into account their presence through VTL:

where AP is the area of the periphery of the solution, dTL is the thickness of the tension layer, and r and n the radius and number of particles contained in the volume of liquid V (which is not the same as the volume of the sample, which would be Vsample = V + Vparticles). Reorganising, the ratio between the effective viscosity and the „intrinsic“ viscosity  of the bulk phase looks similar to Einstein's equation. It also does not appear very different from Taylor's equation for fluid drops with a different viscosity to the bulk liquid:

It is worth stressing that the development proposed starts by assuming that the effective viscosity  is an average of bulk phase and tension layer viscosities, and yet produces the same kind of trend. A likely explanation is that, for the purpose of the example, there is no change in the nature of the inter particle forces. Therefore, an average of the internal “pull around” or cohesion tension (a way to look at viscosity) across the volume between different density regions makes sense for a given chemical composition. The role of surface excesses in fine-tuning the viscosities of the system still needs to be taken into account.

An interesting question is whether an increase in viscosity within the surface tension layer also increases the apparent viscosity of the bulk volume by creating some sort of molecular “bag” which holds the bulk volume together and restricts the mobility of the inside liquid. The response of this “bag” to the mechanical shear stress over a liquid may play a part in the occurrence of the various rheological behaviours found in liquids, suspensions and dispersions, like rheopexy or tixotropy. For example, if the increase in shear streamlines the tension layer molecules, but then as the shear stress decreases the molecules get entangled, this would result in a rheopectic behaviour.

Finally, there is the question of the dependence of (mu)TL with the nature of the surface and any substances adsorbed onto a dispersed phase. Molecules adsorbed onto particles (e.g. clay) may have a surfactant effect (disrupt the tension layer) or thickening (consolidates the tension layer). This viewpoint may be useful when considering the role of various additives in suspension/dispersion/ flocculation technology.